Tax Levies Are Different in CA: The Prop 13 Pie
Tax Districts
Pretend you own a home.
This home is in a city. It is also in a school district. It is also in a fire district, water district, etc.
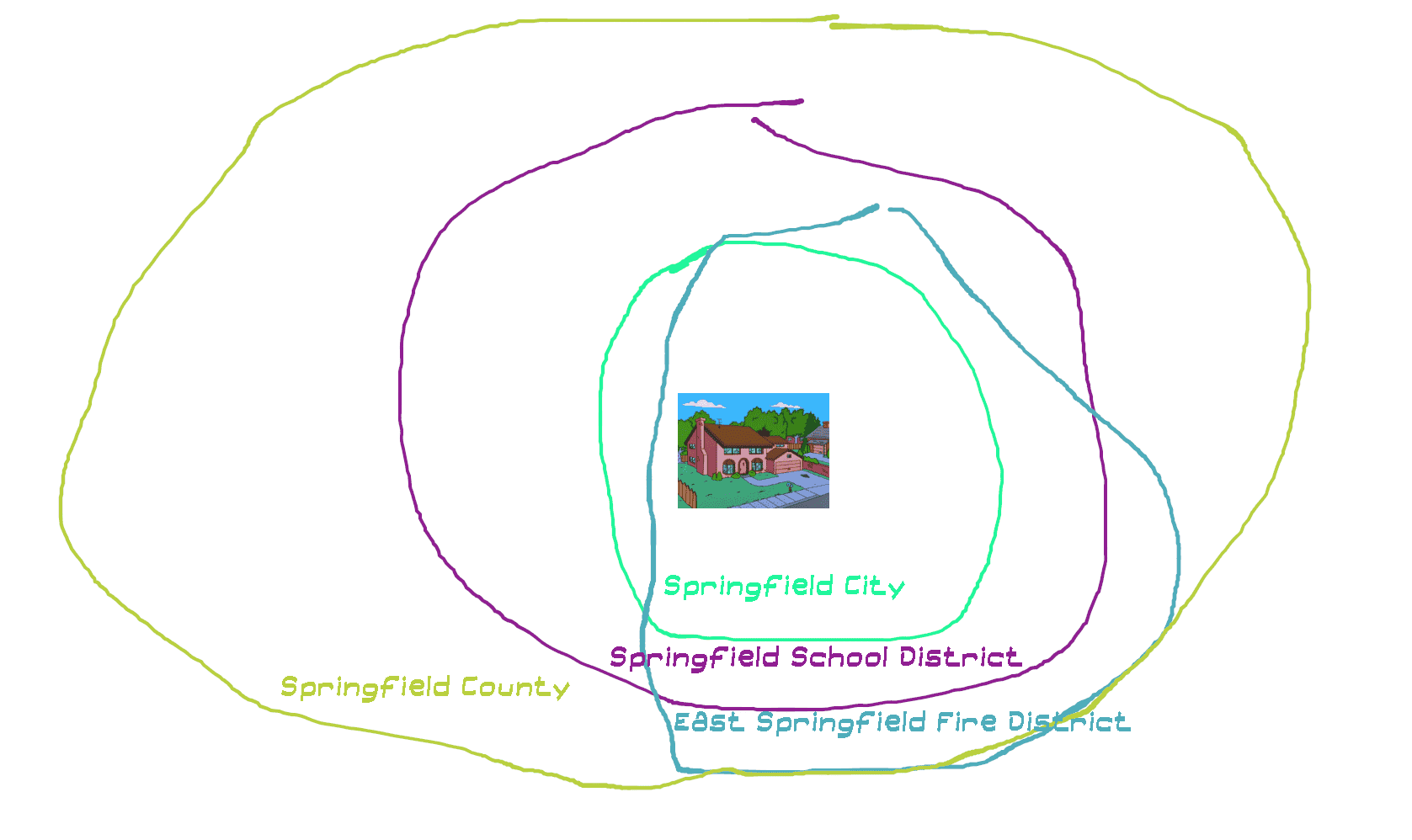
These districts are usually not geographically homogeneous. Kids who live in unincorporated areas still belong to the school district, water districts may span multiple cities, etc.
Normally each district would levy a property tax. The school district levies a 0.3% tax on all properties within the district, and the city levies a 0.5% tax on all properties within the city, etc. So if you owned a home within the city you would pay the city’s 0.5%, the school district’s 0.3%, etc. But if you owned a home outside the city you would not pay the city’s levy and your taxes would be 0.5% less.
In California the Pie is Fixed
California is not normal. California has prop 13. Prop 13 limits the total property tax that and be levied by all entities combined to 1%. Before prop 13 passed, the average total levy for a property in California was 2.67%. All properties are now taxed at 1%. Which means taxing entities can not levy tax across the whole district. Instead they are all now fighting for a piece of a fixed sized pool.
If you own a home outside of a city in California your property taxes are no longer less. Instead your 1% is divided up by fewer interests. The school district or the fire district may get a bigger portion.
On average in Santa Clara county, cities get 9% of the total and the county gets 12%. But there is significant variation.
The Board of Equalization divides the county into tax rate areas. Each area has the 1% tax divided differently.
Every District Takes a Slice
Let’s look at an example.
Here is each city’s share of the 1%
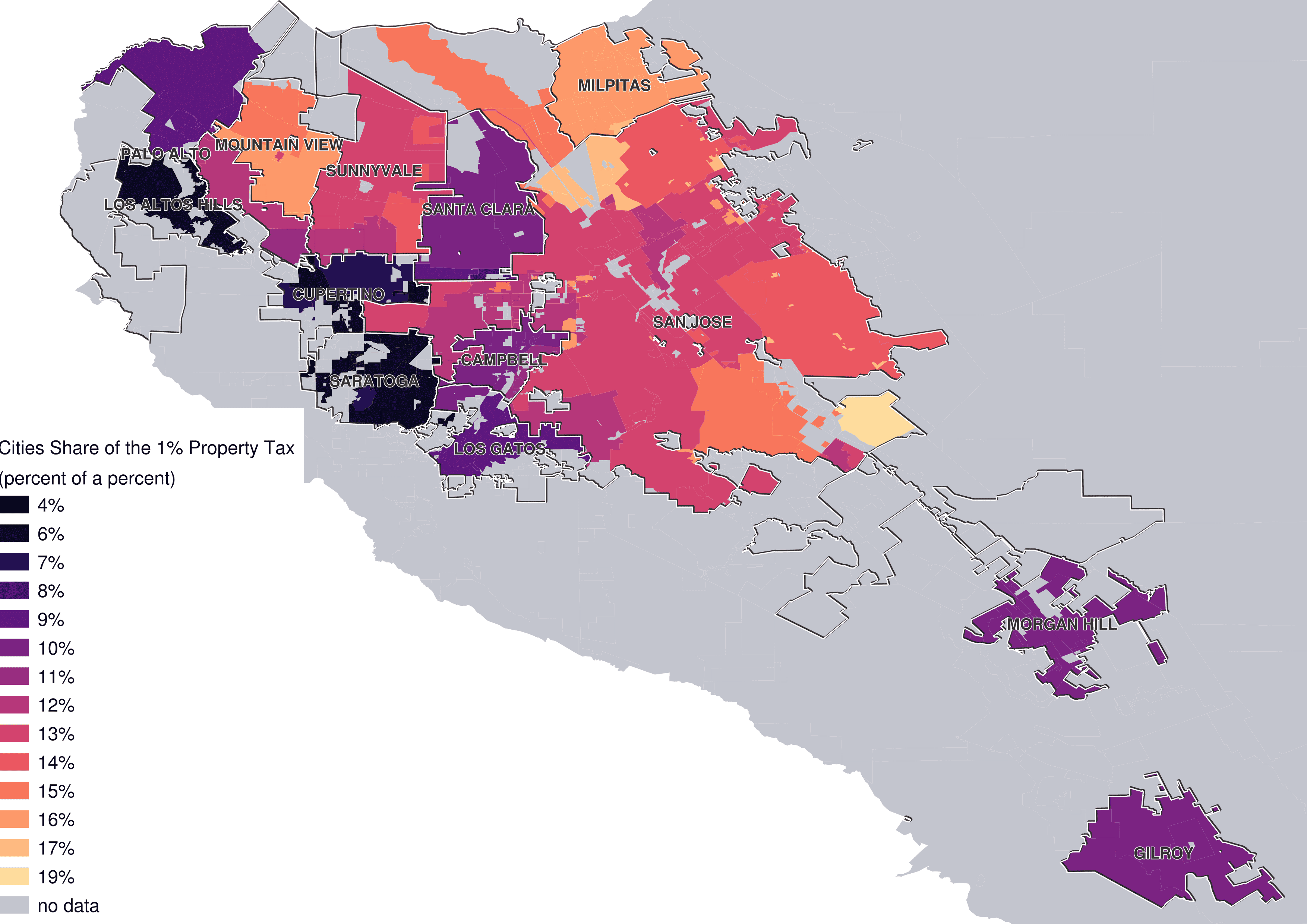
And here is the county’s share.

Notice that in both maps the center of Mountain View has a lower share then the rest of the city. Let’s zoom in.
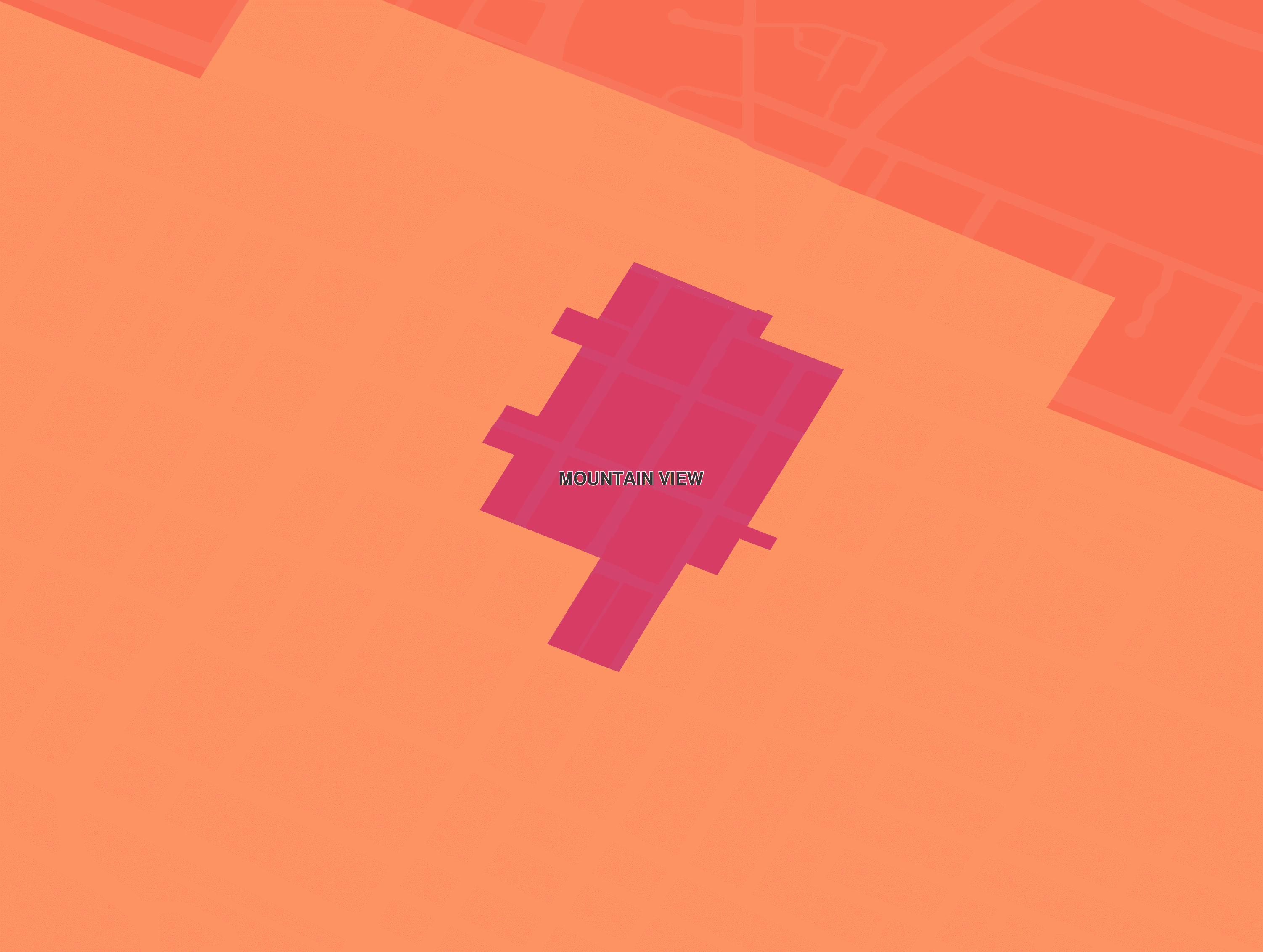
That is downtown. This part of the city has a special parking district. There is a levy on property owners in downtown to help pay for city-maintained parking lots. However, because the city cannot allocate more than the 1% property tax, the levy instead takes a little from everyone else. The 1% limit forces new levies to cannibalize revenue from existing levies.
| Taxing Entity | Downtown Distribution | Distribution Outside Downtown |
|---|---|---|
| Bay Area Air Quality Management District | 0.17% | 0.21% |
| County School Service | 3.11% | 3.86% |
| Education Revenue Augmentation Fund | 15.28% | 15.11% |
| El Camino Hospital | 1.60% | 1.98% |
| Foothill-DeAnza Community College | 5.78% | 7.18% |
| Midpeninsula Regional Open Space District | 1.41% | 1.75% |
| Mountain View | 13.01% | 16.07% |
| Mountain View Elementary | 15.96% | 19.81% |
| Mountain View-Los Altos Union High | 12.92% | 16.04% |
| Mountain View Parking District No.02 | 16.20% | 0% |
| Santa Clara County | 12.80% | 15.81% |
| Santa Clara County Importation Water-Misc District | 0.44% | 0.55% |
| Santa Clara Valley Water District | 0.15% | 0.18% |
| Santa Clara Valley Water District North West Zone 1 | 1.06% | 1.31% |
| Santa Clara Valley Water District West Zone 4 | 0.11% | 0.14% |
In the downtown tax rate area there are 176 parcels, with a total yearly tax revenue of $4.73 million. This generates $766 thousand a year for the special parking district. If the special parking district were dissolved those funds would go to other entities. Mountain View Elementray for example would recieve an additinal $182 thousand a year if downtown were taxed the same as the surrounding area.
Conclusion
My intention here is to illustrate how prop 13 turned property tax levies into a zero-sum game. Property taxes in California are complex. I have a lot more data to analyze, so expect more posts coming soon on this topic. In the meantime if you are wanting to learn more this series from 2016 has good history and analysis.